Tuesday, July 26, 2011

ENGINEERING DRAWING ORTHOGRAPHIC PROJECTIONS

Triangles

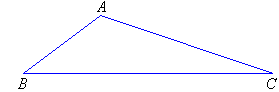
A plane is a flat or level surface in two dimensions.  Figures such as circles or squares have all of their parts lying on a plane and thus, are examples of plane figures. A plane figure on a plane

A triangle is a closed plane figure bounded by three line segments.
A triangle is a closed plane figure
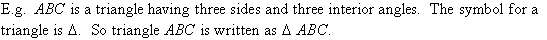
E.g. ABC is a triangle having three sides and three interior angles.
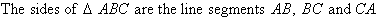
The sides of triangle ABC are the line segments AB, BC and CA.
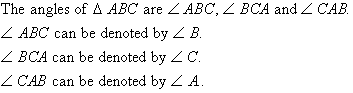
The angles of triangle ABC are angle ABC, angle BCA and angle CAB.
A point where two of the sides of a triangle meet is called a vertex of the triangle. The plural of 'vertex' is 'vertices'. The vertices of triangle ABC are the points A, B and C.


Types of Triangles

Triangles can be classified according to the length of their sides and the size of their angles.


Classifying Triangles according to the Length of their Sides

Scalene Triangles
A scalene triangle has no equal sides.
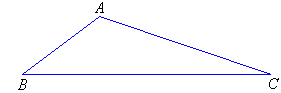
Scalene triangle

Equilateral Triangles
An equilateral triangle has all sides equal.
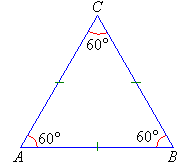
Equilateral triangle
All angles of an equilateral triangle are 60°.

Note:
  • To show that the sides of an equilateral triangle have the same length, we place identical marks on the sides of the triangle.
  • To show that the angles of an equilateral triangle are equal in size, we place identical curves on each angle.

Isosceles Triangles
An isosceles triangle has two sides equal.
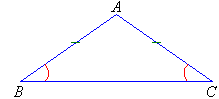
Isosceles triangle
The angles opposite the equal sides are equal.
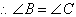
Therefore, angle B equals angle C

Note:
  • In the diagram, side BC has a different length to AB and AC.
  • The side of the isosceles triangle that has a different length is said to be the base of the triangle.  So, BC is the base.
  • Identical marks on the sides indicate that the sides are equal.
  • Identical marks on the angles indicate that the angles are equal.


Example 1

Classify each of the following triangles according to the lengths of their sides:

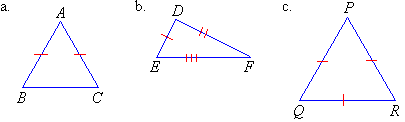
Solution:
Triangle ABC is an isosceles triangle because it has two equal sides. Triangle DEF is a scalene triangle because all three sides are of different length. Triangle PQR is an equilateral triangle because all three sides are equal in length.


Classifying Triangles according to the Size of their Angles

Acute-angled Triangles
An acute-angled triangle has all angles less than 90º (i.e. all three angles are acute).
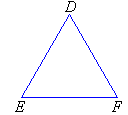
An acute-angled triangle
For example, triangle DEF is an acute-angled triangle as all angles are less than 90°.

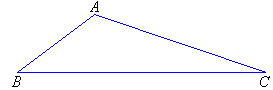
Obtuse-angled Triangles
An obtuse-angled triangle has one angle greater than 90º.  That is, one angle is obtuse.
An obtuse-angled triangle
For example, triangle ABC is an obtuse-angled triangle as angle BAC is an obtuse angle.

Right-angled Triangles
A right-angled triangle has one angle equal to 90°.  That is, one angle is a right angle.
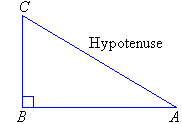
A right-angled triangle

Note:
  • The side opposite the right angle is called the hypotenuse.
  • The hypotenuse is the longest side of the triangle (which can be verified with a ruler).


Example 2

Classify each of the following triangles according to the size of their angles

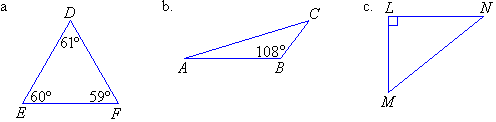
Solution: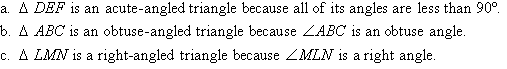
Triangle DEF is an acute-angled triangle because all of its angles are less than than 90º. Triangle ABC is an obtuse-angled triangle because angle ABC is an obtuse angle. Triangle LMN is a right-angled triangle because angle MLN is a right-angle.


Activity 1

Complete Activity 1
Posted by at
Labels:

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)